
Orthomanuele Geneeskunde
Orthomanuele Geneeskunde

Biomechanica
Symmetrie en asymmetrie.
De symmetrie in biologische structuren is van wezenlijk belang voor het functioneren.
Gepubliceerd in "SPORTGERICHT" vakblad voor leraren lichamelijke opvoeding.
Vakblad voor training, onderwijs en wetenschap
57e jaargang - nummer 5 - oktober 2003
Leven is het ultieme voorbeeld van werkende complexiteit.
Een universele reeks van bouwregels lijkt als leidraad te dienen voor het ontwerp van organische structuren. Deze leidraad is er zowel voor eenvoudige koolstofverbindingen als voor complexe cellen en weefsels.
Een organisme (bacterie, paard of mens) ontwikkelt zich door een onnavolgbare opeenvolging van interacties. Hierbij wordt gebruik gemaakt van een vast aantal verschillende componenten. Deze componenten, of subsystemen, zijn opgebouwd uit kleinere moleculaire bouwstenen, die onafhankelijk van elkaar, hun eigen dynamisch gedrag vertonen.
Een voorbeeld van het dynamisch gedrag is de mogelijkheid om chemische reacties te katalyseren.
Wanneer deze bouwstenen worden gecombineerd in een wat grotere functionele eenheid, zoals in een cel of in een weefsel, dan ontstaan echter volslagen nieuwe en onvoorspelbare eigenschappen.
Daartoe horen bijvoorbeeld ook het vermogen om te bewegen, van vorm te veranderen en te groeien.
Alle levende organismen worden gemaakt van dezelfde bouwstenen: respectievelijk gaat het om C, H,O, N en Ph. atomen. Het enige onderlinge verschil is gelegen in de positionering van bovengenoemde atomen.

Zolang er leven is op aarde past de natuur eenvoudige assemblageregels toe.
Dit gebeurt in een zich continu herhalend patroon.
Een herhalend patroon vanaf de kleinste, eenvoudige moleculaire structuren tot aan de grootste complexe weefsels. De bouwwerken worden opgebouwd met; spiralen, driehoeken, viifhoeken, zeshoeken.
Het fenomeen waarbij componenten samengaan om grotere, stabiele structuren te vormen, die nieuwe eigenschappen hebben en niet voorspelbaar zijn uit de onderdelen waaruit ze gemaakt zijn, staat bekend als het zelfassemblerend vermogen.
In het menselijk lichaam gaan grote moleculen zich samenvoegen in cellulaire onderdelen, bekend als organellen.
Cellen voegen zich samen tot organen etc.
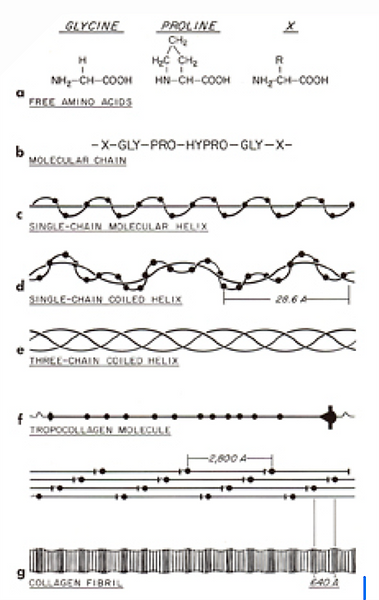
Weefsels worden geweven als zijden draden in een kledingstuk door diverse collagene vezels.

Het resultaat ervan is, dat een lichaam wordt opgebouwd als een laag na laag gestapeld systeem. Een systeem dat zelf weer een onderdeel is van een groter systeem.
We weten maar weinig over het mechanisme dat de moleculaire opbouw regelt. We weten echter nog minder van het samengaan van groepen moleculen tot levende cellen en weefsels.
Van de "krachten" die in de diverse groeperingen uitgeoefend worden weten we eveneens zeer weinig.


Filamenten opbouwen met micro tubuli
Ingmar Heytze verwoordde het als volgt:
“Atomen klitten samen om een tijdje jij en ik te zijn, totdat alles wordt herschikt.”
Het zelf-assemblerend vermogen van de mens.
Tensegrity is een begrip dat verbonden is aan de bovengenoemde krachten. Het begrip tensegrity refereert aan een bouwsysteem uit de architectuur. Het gaat hier om een bouwsysteem waarbij het bouwwerk zichzelf stabiliseert.
Dit laatste is gebaseerd op het feit dat de trek-spannings en compressie-krachten op een bepaalde wijze zijn verdeeld over het hele bouwwerk.
Tensegrity als basis voor het zelfassemblerend vermogen was al bekend voordat men de dubbele helix-opbouw van het D.N.A
op het spoor kwam. Het begrip is een samenvoeging van de Engelse woorden: Tension en Integrity.
Tensegrity eigenschappen.
Tensegrity structuren hebben enkele kritische eigenschappen gemeen:
1. Tensegrity structuren zijn mechanisch stabiel.
Niet vanwege de stabiliteit van de onderdelen, maar vanwege
de structuur van het gehele bouwwerk.
2. Trek- en drukkrachten worden over de héle structuur verdeeld.
Het bouwwerk vindt daardoor zijn eigen balans.
3. Een toename in spanning in een bepaald deel, resulteert in
een toename van de spanning in andere delen.
Dit gebeurt zèlfs in de tegenoverliggende onderdelen.
Deze alles omvattende toename in trekspanning wordt in
evenwicht gehouden door een toename van compressie in de
steunbalken !
4.Trekspanning (energie) verplaatst zich over de kortste afstand
tussen twee punten!
Daarom zijn tensegrity structuren uitermate precies geplaatst.
Dit om de van buitenaf komende krachten op te vangen.
Zij geven een maximum aan sterkte, gegeven de massa van het
materiaal.
5. Tensegrity vindt plaats door het hele lichaam.
Op bijna alle denkbare niveaus.
De bouwstructuren.
In zijn grondvorm onderscheiden we een opbouw van frames met steunbalken. Het gaat om een systeem waarbij elke balk trek- en drukkrachten kan opvangen. De balken zijn zodanig met elkaar verbonden in driehoeken, vijfhoeken of zes- hoeken, dat zij elkaar op de verbindingspunten fixeren.
Daarmee bewerkstelligen ze een gewaarborgde stabiliteit.

Het is een constructie waarbij het systeem van de spankabels de trekspanning opvangt en waarbij het systeem van de harde delen de drukkrachten verwerkt. Het geheel is te vergelijken met een tent met tentstokken en scheerlijnen. Voordat er van buitenaf kracht op dit systeem wordt uitgeoefend, is het gehele systeem al onder trekspanning en drukkracht gebracht.
(préstress of voorspanning.)


Tensegrity in het menselijk lichaam.
{Alles over Tensegrity in de paragraaf hierna.}
De ± 206 menselijke botten worden bij de mens verbonden door structuren die te vergelijken zijn met spankabels.
De botten fungeren als steunbalken. De spieren, banden, kapsels e.d. als préstress spanningsdragers.
Alle structuren zijn geweven uit diverse collagen vezels met eigen specifieke kenmerken.
Als een gebreide trui, een linnen laken of een zijde kimono.
Er zijn genetische afwijkingen zoals bij bv. de ziekte van Marfan waarbij aangeboren bindweefsel zwakte bestaat.


Op microscopisch niveau zijn het de eiwitten, die samen met andere sleutelmoleculen, zichzelf stabiliseren. Mensen, planten en dieren zijn geëvolueerd tegen de zwaartekracht in.
Voor de anatomische bouwwijze en de mechanische basisprincipes vormt dit geen enkel probleem.
100 miljoen jaar geleden hadden we, onder vergelijkbare omstandigheden, reeds zwaardere voorgangers in het dierenrijk.

We zien hier het verschil tussen mechanica en biomechanica.
Spieren zijn zèlf regulerende kabelspanners.
Dat komt in de bouw, gewone mechanica, niet voor.
Spieren zijn zowel effector (veroorzaken spanning),
als sensor (registreren spanning).
De sensor kan bovendien qua gevoeligheid van instelling veranderd worden. (Hierover later.)
Een intrafusale, zichzelf regulerende sensor, die via de extrafusale spieren tevens effector is. De regulatie van de spierspanning vindt op diverse neurologische niveaus plaats.
Via de feedbacklus van het extrafusaal spierweefsel, via de gamma motorische-lus naar de intrafusale spiervezels.
ie plaatje het Y regelsysteem hieronder.
Conclusie:
Spierspanning kan dus “onbewust” opgewekt en gereguleerd worden!!!
Indien de voorspanning en het regelbereik bepaald kunnen worden door het organisme zelf, dan is de vraag:
- Wat is dan de uitgangswaarde?
- Welk referentiekader wordt er gebruikt?
De uitgangswaarde van de spierspanning wordt (net zoals in het gehele chemische en biologische regelsysteem) fundamenteel gebaseerd op: Laag energetische stabiliteit.
Dit is een grondbeginsel in de chemie en biologie. Een onnodig hoger energieniveau kost meer zuurstof en meer voedsel en bedreigt derhalve het voortbestaan.
De werking van het regulatiesysteem.
Stel er komt een energetische krachtgolf het lichaam binnen.
We springen bijvoorbeeld van een tafel. De energiegolf loopt in dit voorbeeld van caudaal naar craniaal. (Van de voeten naar het hoofd toe). De schok wordt daarbij via de tensegritystuctuur van banden, spieren en botten geabsorbeerd.
De energetische impact verloopt via de grote driehoek, vijfhoek en zeshoekstructuren naar de kleinere driehoek, vijfhoek en zeshoekstructuren. Uiteindelijk mondt het uit in de kleinste moleculaire pentagons en hexagonen.
Tensegrity schematisch naar dieper gelegen structuren.
Dus van buiten naar binnen en van grote veelhoeken naar de kleinere. Hierbij wordt de meeste energetische kracht geabsorbeerd door compressie van de botten.
Dit, omdat trekspanning in een tensegrity systeem ten alle tijden wordt omgezet in compressie in de steunbalken.
Je ziet bij regelmatig grote belasting, bijv. bij gewichtheffers dat zowel in de botmassa als in de botstructuur veranderingen optreden. De energetische golf dooft in het lichaam normaliter, qua intensiteit, gelijkmatig uit. Als een golf over het strand. In steeds kleinere veelhoeken.
Een op een tensegrity structuur binnenkomende kracht verdeelt zich echter alleen dan gelijkelijk, als de afstanden van de spankabels precies gelijk zijn.
Zo niet, dan gaat 100% van de energiegolf over de kortste weg!
Als de energiegolf botst op een asymmetrische structuurlaag wat dan ?
Trekspanning wordt voortgeplant over de kortste afstand tussen twee botten. Dit verloopt volgens de alles of niets wet. Hier kiest de krachtgolf dus een bepaalde richting. Dit resulteert dan in een piekbelasting op het aankomstpunt.
Relatief gering in de kleinere structuren, relatief groot in de grotere.
Als er meerdere asymmetrieën aanwezig zijn, dan ontstaat er zelfs een enorme energetische piekbelasting op een structuur
die daar niet op berekend is.
Dit levert voor het lichaam een bedreigende situatie op. Bovenstaande situatie kan ontstaan als b.v. een bekken scheef staat. De energetische krachtsafwikkeling is dan verstoord.
De binnenkomende kracht kan niet gelijkelijk verdeeld worden.
Het systeem kan derhalve decompenseren.

De biomechanica behoeft een driedimensionaal model.
Je ziet bij A, dat er vijf scheerlijnen c.q. spandraden vertrekken.
Als de kracht bij A binnenkomt dan wordt deze energie,
tenminste als het model symmetrisch is, over vijf lijnen verdeeld.
Volgens de rekensom:
100% Energie gedeeld door 5 = 20 % Energie.
Het eerstvolgende station waar de energie binnenkomt krijgt derhave 20% E van de originele energie.
De energiegolf c.q. kracht die dan in de stations B 1,2,3,4,5 aankomt is 1/5 van de totale impact.
Wat ook duidelijk in het model te zien is, is dat er lijnen naar dieper gelegen balken gaan. Hierdoor kan de energie c.q. kracht in de diepere structuren mede opgevangen worden.
De energiereductie verloopt naar de kleinere hexagonen als een soort "Droste cacaobus-effect".
In feite loopt de energie door tot op intracellulair niveau, uitmondend in de "van der Waals" krachten.
Veel van de energieopvang vindt, zoals al eerder gezegd, plaats in de botten. Bij veel kracht absorptie veranderd de dichtheid van botweefsel.
Dit is een fysiologische aanpassing.
Gewichtheffers hebben een veel dichtere botstructuur dan zwemmers of wielrenners.
Je kan na de éérste asymmetrie dus al 80% van je eerste opvangcapaciteit kwijt zijn! Station B krijgt niet 20% maar de volle 100% te verwerken.
Een en ander is afhanklijk van het aantal spankabels dat in de eerste opvang participeert.
Bovendien speelt het lengte-verschil tussen de kabels een rol.
Bij een tweede asymmetrie verlies je mogelijk meer dan 96% van je originele opvangcapaciteit. (20% : 5 = 4 %
in het derde station C, etc. etc.)
Het is te vergelijken met een motorhelm.
De klap is gelijk groot met of zonder helm, echter de verdeling over het oppervlak geeft de beschermende werking.
Je krijgt geen puntbelasting.
Asymmetrieen in de diepere lagen kunnen waarschijnlijk beter gecompenseerd worden. De totale hoeveelheid energie is dan immers al sterk gereduceerd.
De reactie op een asymmetrische impact.
Het lichaam gaat zich tegen een dergelijke asymmetrische impact actief verdedigen. Station C kan niet meer verdragen dan 10%.
Het gamma motor reflex systeem verandert de lengte van de langste spankabel zodanig, dat er door de spiercontractie toch een symmetrie ontstaat. (Pseudo-symmetrie)

Het Y regelsysteem.
De scheerlijnen (spieren) naar de hoekpunten worden even kort gemaakt. Het is een proces van selectieve hypertonie.
(Ergo de diagnose: Hamstring is te kort, is niet juist.
Hij is juist actief hypertoon. De hypertonie corrigeert de bekken - foutstand of knie-foutstand. Een biologisch regelsysteem.!!

De spieren aan de rechterkant gaan samentrekken om de scheefstand te verminderen.
Het spier verdedigingsmechanisme is niet specifiek.
Spiertonusverhoging gebeurt ook bij bijvoorbeeld eenzijdige zenuw- prikkeling. Het lichaam wordt dan als verdedigingsreactie naar de niet aangedane zijde getrokken.
Bij sterke zenuwoverprikkeling, doen veel spiergroepen mee, met als gevolg dat alles als een korset wordt vastgezet. We kennen dit spierverzet "defense musculair" ook van andere situaties b.v. bij ontstekingen, bij sterke vibraties, bij koorts en bij sterke geluiden.
Spieren kunnen vele jaren hypertoon zijn, met als gevolg:
- de aanhechtingsplaatsen (origo en insertieplaatsen)
(periost = botvlies) worden overprikkeld, we zien hier
"fysiologische" botgroei optreden.
- de spierfysiologie verandert,
botstukken komen door de spanning in een andere
(fout)stand te staan.
- Bot groeit in de richting van de trekkracht.
Deze "artrose" is op X ray aantoonbaar.
Deze botgroei is op zichzelf weer een beschermings-mechanisme! (het verbetert de insertie) Met andere woorden het verdedigingsmechanisme zorgt voor een:
Hoog energetische, gebalanceerde pseudo-symmetrie.
Bij een langdurige hoge spierspanning, door welke oorzaak dan ook, ontstaat er een hypertone vicieuze cirkel.
Door een verkeerde houding, door een scheefstand of een verdedigingsstand (door b.v. wortelprikkeling of asymmetrie) ontstaat een dergelijk abnormale spierspanning.
Deze spanning veroorzaakt prikkeling in het spierweefsel onder andere door verzuring. Via allerhande feedback mechanismen, die elkaar continu versterken en beïnvloeden ontstaat een chronische overprikkeling.

Er is géén ontspanning, slechte weefselverversing, verminderde zuurstof toevoer. De vraag is nu, wie kan er en op welke wijze, deze vicieuze cirkel doorbreken?
Welke preventieve maatregelen zijn noodzakelijk ter voorkoming van een recidief?
Ortho Manuele Geneeskunde. OMG
Het doorbreken van de vicieuze cirkel kan alleen door een
inhibitie (-) te bewerkstelligen in het zichzelf versterkende en instandhoudende cirkel - mechanisme. Dit kan o.a. door spierverslappers. Deze werken àspecifiek en pakken niet de oorzaak aan. Het middel zal dan ook snel zijn effect verliezen.
Manuele geneeswijzen pretenderen de oorzaak aan te pakken d.m.v. het toepassen van een inhibitiereflex op de spierspoel, waarbij tevens het lichaam in balans wordt gebracht.
Indien dit op de juiste manier wordt gedaan en er eveneens de recidief voorkomende instructie wordt gegeven, is dit de meest afdoende methode. Ergens een “kraak” zetten of aan de nek trekken is niet alleen obsoleet, het is letterlijk en figuurlijk
“Non Sense”
Massages zijn heerlijk en nooit contra- indicatief. Ze werken alleen niet causaal.
Dit laatste geldt ook voor warmteapplicatie, saunagebruik e.d.
Uit het icosahedron model is begrijpelijk te maken dat fout- standen hun invloed kunnen doen gelden op verderweg gelegen delen.
Prof.Karl Lewit stelde, op het schoudercongres in Eindhoven (2002), dat een schouderprobleem kon ontstaan door een fout in de bekkenstand of een fout in de heupstand. Door de spanning op de buikwand te verhogen, middels een korset, kon de patiënt haar schouder weer bewegen.
Het korset zorgde voor herstel van de spannings- integriteit.
Het is moeilijk voor te stellen dat een fout in de heupstand aanleiding is voor schouderklachten. Makkelijker is het voor te stellen dat als de voorpaal van een tent scheef staat, het tentzeil achter niet goed zit.
Correcties met de scheerlijnen helpen wel iets maar niet afdoende. Artsen en therapeuten zoeken de oorzaak meestal daar waar het pijn doet. Dit ligt voor de hand, maar het blijkt vaak niet te kloppen.
Gecompenseerde asymmetrieen geven vaak aanleiding tot klachten ergens anders in het lichaam. Ze zijn meestal de oorzaak van de vicieuze dysfunctie-cirkel. De klachten kunnen schijnbaar plaatsvinden tot op orgaanniveau toe.
De vraag is: zijn dat, door het geprikkelde zenuwweefsel, sensaties die naar het orgaan verwijzen of doet het orgaan daadwerkelijk mee? Een “spanningsfout” van thoracaal 4, geeft regelmatig aanleiding tot hartkloppingen, die bij houdings- verandering kunnen veranderen.
Het orgaan doet hier dus wel degelijk mee.
Een tweede vraag die je kunt stellen heeft betrekking op duur van het effect. Dit is moeilijk te beantwoorden. De spierspanning die inwerkt op de wervels en andere botstukken verandert in de tijd. Soms snel, soms pas na jaren. Soms zijn wervels eenvoudig te resetten, soms lukt dat niet. Soms reversibel en soms irreversibel zoals bij een scoliose!!.

Bij scoliose zie je zelfs dat het witte dynamische spierweefsel in de rug (convexe zijde) omgezet wordt in rood spierweefsel.
Dit is een aanpassing om langdurige spanningen aëroob te kunnen volhouden. (Guyton, Medical Physiology)
Een fout staand sleutelbeen geeft vaak maagklachten, een fout staande atlas, duizeligheid en oorsuizen. Een bekkenverwringing pseudo-radiculaire uitstraling in het been etc.
De vraag voor velen van ons is, of dit soort inzichten op korte termijn zal leiden tot andere opvattingen in de geneeskunde?
Een Engelse zeekapitein meldde reeds rond 1500 dat het eten van citrusvruchten scheurbuik kon voorkomen. Toch heeft het 250 jaar geduurd voor men het algemeen accepteerde.
Na een langdurige asymmetrische stand zal na correctie enige tijd nodig zijn voor herstel.
Oefeningen en spiertraining hebben in deze fase géén zin.
Net zo min spiertraining geen zin heeft bij een verstuikte enkel of een geïrriteerde zenuw. Pas indien het herstel van zenuwweefsel, kapsels een feit is, is spierversterking, ter voorkoming van een recidief, zinvol. Onbelaste training b.v. zwemmen kan nooit kwaad. Ook al kan dat zelfs pijnlijk zijn.
Verantwoording.
De opvattingen die in dit artikel zijn weergegeven zijn niet gebaseerd op een strikt wetenschappelijke verantwoorde zienswijze. Het is eerder een vorm van fenomenologie, gebaseerd op kritische waarnemingen uit de praktijk, onderdelen uit de wetenschap, analyses vanuit een duidelijk andere invalshoek en door het combineren van allerlei gegevens. Het concept heeft volgens mij wel een hoog waarschijnlijkheidskarakter. Het heeft interessante consequenties voor zowel de sportgeneeskunde als de manuele- geneeskunde.
Literatuur:
1. The Architecture of Life, D.E.lngber, scientific American, Jan.
1998, P.30-39 On Growth and Form. Revised edition.
D’Arcy W.Thopson. Canbridge University Press, 1942 (reprited
1992)
2. Movement and Self-control in Protein Assemblies.
D.L.D.Caspar, In Biophysical Journal. Vol.32, no 1
Page 103 -138; October 1980
3. Cellulair Tensegrity, Defining
New Rules of Biological Design That Govern The Cytoskeleton.
D.E.lngber in Journalof Cell Sclence, Vol.’04, No.3, pages
613.627; March 1993.
4. Geometric Control of Cell Life and Death, C.Schen e.a. in
Science, VOL.276, pages 1425-1428 May 30, 1997 S.
5. Tensegrity, The Architectural Basis of Cellulair
Mechanotransduction. D.Ingber in Annual Review of
Physiology, Vol 59, pages 575.599; 1997
6. Synergetics. R.B.Fuller. New Vork, Mc. Millian 1975; 104,
354.355, 372.420 The icosahedron as the three- dimensional
finite element in biomechanica I support. S.M.Levin
Society of General SystemsResearch, 1986, page G14-G26
7. First supraspinal control of mammalian muscle spindies extra-
and intrafusal coactvation, R.Granit e.a. in Journalof Physiology,
(London), ‘47’ 385,1959
8. Receptor Function of the Muscle spindie. Textbook of Medical
Physiology, AC.Guyton,Saunders Company
9. The innervation of the knee joint.Freeman, Wyke. An anatomical
and histological study in the cat. Journal of Anatomy
(London) 101 (1967) pag.505.
10. Neurphysiology der Gelenke und der Musculatur. Manuelle
Medizin, Dvorak & Dvorak, Thieme Verlag.
11. Geschichte der Manuelle Medizin. A.Cramer, e.a. Springer
Verlag Manuelle Medizin, Diagnostik. Dvorćk & Dvorćk,
Thieme Verlag.
12. Van Quantum tot Quark. Inleiding tot de quantummechanica,
golven en deeltjes. G.’t Hooft. Teleac, 1989
Ale van der Veen

Paul Delvaux
The Geometry of Anatomy
The Bones of Tensegrity
Among clinicians and bodyworkers today, there appears to be a great deal of interest in the concept of tensegrity as it
applies to living forms, but much confusion as well. In some circles it seems to be the flavour of the decade but what
are they talking about? What exactly is a tensegrity? Is it a useful scientific description and explanation for anatomical
function? Or is it just a metaphor for the intuitive feeling that bodies behave as whole systems held in connective
tension? If the latter, it’s as good or better than any other analogy and the definition can remain vague. But if
tensegrity claims to explain the biomechanics of living structure, then more is required. A clear definition of
“biotensegrity”and a means to test the hypothesis is needed. The actual relations between tension and compression
components in the body need to be examined. Can biotensegrity help explain the complex interplay of these forces in biomechanical terms and if so what does that imply? One mark of a valid scientific hypothesis is its predictiveness.
If tensegrity provides better descriptions, does that make for better prescriptions?
I’m not an anatomist, a biomechanist, or a body worker. I’ve come to this work as a geometer with fresh eyes and new
ideas. I make tensegrities for a living and for pleasure – toys, furniture, sculptures, mobiles and biotensegrities, and the
focus is always on how something is built. I pay attention to details. In the case of living things, I’ve tried to apply
what I’ve learned about the geometry of structure to, in effect, reverse engineer evolution. I’m looking for the most
material and energy efficient strategy to organize and design self assembled, strong, resilient, repairable, flexible,
lightweight mobile frameworks.
Quite a mouthful, but put this way, I can focus on the geometry of the body and speculate on how and if, it is
composed of patterns identifiable as tensegrities.
My tensegrity models are abstractions of the body designed to approximately diagram forces and movements that act
on anatomical structure. Looking for a close match in form and function, I have attempted to model human form and
function using only this principle. Many iterations later I’m still testing the hypothesis
Tensegrity Skeleton

Tensegrity geometry is a language I’ve used to interpret and represent anatomic form as a dynamic interplay of forces
in four dimensions (bodies moving through time). What I've found out is intriguing– movement and degrees of
freedom in the models seem roughly analogous to human movement and freedom. In addition, changes to one part of
the model (e.g. local increased tension) are reflected throughout the structure; this is similar to the observation that
pain in the body often occurs at a distance from the source of insult. This is suggestive but it isn’t proof. Beginning to
work out the details of the theory is what this paper attempts to address.
Tensegrity is...
Tensegrities are all about tension and compression.
Every structure, whether an artifact created by intelligence or a
living form evolved by natural selection, is a balance between these two and only these two forces. Engineer and
architect Mario Salvadori points out in his book Why Buildings Stand Up, that shear is equivalent to tension and
compression forces acting at right angles and is not a separate force.(1)
Tensegrities are special case structures where the play of these two forces is visible in the design.
But tensegrity is also certainly one of the most powerful memes in the modern era. I think this is because of the elegance and power tensegrities have to describe and illustrate the behaviour of whole systems as fractals.
Tensegrity is a potent metaphor for envisioning existence in syncretic and non–atomistic ways. It has come to be imbued with multiple meanings at many levels of intercourse…
Carlos Castaneda appropriated the term as… “The name given to the modern version of the magical passes: positions
and movements of body and breath that were dreamt and stalked by men and women seers who lived in Mexico in
ancient times…”(2)
It turns out that Castaneda admired R. Buckminster Fuller who coined the term; he then borrowed and copyrighted the word for his own purposes.
The Canadian theoretician Stafford Beer, the founder of Management Cybernetics also admired Fuller and used
tensegrity as a social metaphor to describe complex decision-making relationships in groups. He coined the term
Syntegrity as tensegrity had already been copyrighted…
The Wikipedia weighs in with, “Tensegrity is a portmanteau of tensional integrity. It refers to the integrity of structures as being based in a synergy between balanced tension and compression components.”(2) Synergy refers to the
observation made first by R. Buckminster Fuller that in any system the whole is always greater than the sum of its
parts. The behavior of tensegrities is a visual demonstration of this.
How does Fuller define it? From Synergetics 700.011:
“The word tensegrity is an invention: it is a contraction of
tensional integrity. Tensegrity describes a structural relationship principle in which structural shape is guaranteed by
the finitely closed, comprehensively continuous, tensional behaviors of the system and not by the discontinuous and
exclusively local compressional member behaviors.”(3)
Easy for him to say… Fuller went on to design the largest
enclosed domes ever built utilizing tensegrity principles.
The sculptor Kenneth Snelson who made the first tensegrity structures in 1948 called them something different. In an
interview he said, “Tensegrity, the word, has become so confusing through multiple uses that it calls any definition
into question. This is the reason I've long advocated Floating Compression… "It" describes a closed structural system
composed of a set of three or more elongate compression struts within a network of tension tendons, the combined
parts mutually supportive in such a way that the struts do not touch one another, but press outwardly against nodal
points in the tension network to form a firm, triangulated, prestressed, tension and compression unit. Why triangulated? The reason is that it's possible to build such a structure whose network is non-triangulated. Such structures are flaccid and decidedly not firm.”(4)
In the art world Snelson is well known and his floating compression sculptures are found in galleries, private collections, and museums around the world.
A tensegrity requires at minimum three conditions to fit either Kenneth Snelson's or Buckminster Fuller's definition.
1.) A continuous connective tensioned network supports discontinuous compression struts. Snelson insists that struts
must be free floating in a web of tension and not touching.
A geodesic dome, which Fuller considers to be tensegrities,
has multiple compression struts meeting at central hubs but they are discontinuously connected, that is, they do not
transfer compressive loads. In these domes it is the tension forces that travel along the outer edges of the struts that are
continuous. Similarly, if anatomical structures operate as tensegrities, then in most orientations the bones do not pass a
direct load across the joint– rather the tension members; ligaments, tendons, and fascia transfer loads and the bones
float in this tension matrix.
2.) All tensegrities are prestressed under tension; they are self–supporting and independent of gravity. But the weight
of the structure also adds to the prestress. As you increase the weight load the tensegrity tightens and gets smaller. The
heavier the structure is, the greater the tension, and the less the range of motion. This presents real design problems
when trying to model living systems that have and use joints with multiple degrees of freedom. My models for
example can emulate biologic movement because I use elastic tension nets that are taut enough to maintain the shape
of the model yet have enough residual elasticity to move through a wide range of positions. When the size and weight
of a model increases, so does the prestress. It is always surprising to discover how high the tension levels climb when
building large tensegrity structures. In some of Snelson’s largest sculptures (50’–100’) the tensile cables carry
thousands of pounds of force. To make human scale tensegrity models that articulate and are prestressed is not a trivial
challenge.
3) Tensegrities are self–contained non–redundant whole systems. All components are dynamically linked such that
forces are translated instantly everywhere; a change in one part is reflected throughout. These features distinguish
tensegrities from all other tension structures, e.g. a radio mast or a sailboat’s mast is fixed at the base and needs that
fixed point to keep it upright. The boat does not need the mast for it’s integrity but the reverse is not true. Every part in
a tensegrity is reliant on the entire structure for its continued existence. In terms of living forms, a discontinuity in a
structure marks the boundary or interface between separate tensegrities. Also, molecules within cells within tissues
within organs within bodies, and bodies within environments are all synergistically linked tensegrities in a hierarchical
cascade from the smallest wholes to the largest.
At the macro scale of human anatomy, I see tensegrity as a diagrammatic way to model in four dimensions forces
acting on complex shapes in terms of stress vectors. I suggest that this analytic technique can explain the structure of
individual bones as well as aggregates that make up the body. Tensegrity in this sense is an applied principle– a map
of the nature of structure. If tensegrity is seen not so much a building system as it is a description of the most efficient
way that all form is organized, in terms of most economical use of energy and material, then we would expect
parsimonious nature to utilize this principle universally. The task is to determine exactly how this might have been
achieved at each scale of the continuum.
Biotensegrity
In the last 25 years tensegrity has come to be associated with various inquiries into the nature of living structure.
Donald E. Ingber MD PhD, Professor of Pathology at the Harvard Medical School, has done cellular research that has
been widely reported in major scientific journals as well in Scientific American, The Architecture of Life, January 1998.
He has found conclusive evidence that tensegrity provides the best explanation for the cytoskeleton of the cell,
its movement and behavior.
Stephen Levin M.D., an orthopedic surgeon who coined the term biotensegrity has applied the principle to macro scale anatomy in papers and numerous lectures around the world for over 25 years. His vision of biomechanical biotensegrity is radical and comprehensive. (biotensegrity.com). Others such as Tom Myers, well known writer and teacher of Structural Integration (http://www.anatomytrains.us/), and George Roth a writer and
chiropractor from Toronto (http://www.matrixinstitute.net/) both use the term in helping explain their practice and
methodology but the usage is general and mostly metaphoric. There are many others writing on this subject, but not
everyone understands tensegrity in the same way.
And some clearly understand less…
In a paper for an osteopathic journal, an American osteopath used tensegrity to model cranial sacral work but labeled a
picture of a train trestle bridge an example of tensegrity. The trestle bridge is an open braced framework– a truss that
conveys forces to the ground through the compression members– this disqualifies it as a tensegrity. A physiotherapist
interested in the concept thought that a spider’s web was a tensegrity structure. But a spider’s web is arranged the
same as a trampoline– a flexible tension membrane suspended from an exterior framework which is independent of the
membrane. The branch doesn’t rely on the web for support but the web needs the branch. Individual tensegrities are
integral– all parts are connected in a non–hierarchical relationship. A body worker who uses tensegrity as a metaphor
compares it to a mast in a sailboat. But a ship’s mast acts as a lever arm whose fulcrum is the deck of the boat (which
doesn’t rely on the mast for its integrity) and is prevented from tilting by tension shrouds. Tensegrities have no lever
arms or fulcrums in the classical sense. Forces are transferred globally across the entire structure. A well–known teacher of yoga teachers, who talks about tensegrity in her instruction, thought she lives in a tensegrity house because it had triangular roof sections. She no doubt has a stable roof but it isn’t a tensegrity. Each of these clinicians has used
tensegrity as an analogy based upon tension structures or stability through triangulation to describe their work but no
one is using the term correctly. All tensegrity structures are tensile but not all tensile structures are tensegrities. As we
are bound together with connective tissue that acts in tension, it is legitimate to ask what kind of tensile form we are.
Geometry of Tensegrity
The yoga teacher was partly right; it is about triangles. The only way to fully stabilize and constrain any structure is by
triangulating surfaces or cavities in compression and/or tension in all three dimensions. This fact may not be obvious
at first as many artifacts conceal their triangulation within their form such as the square walls and roofs of buildings.
Tensegrity structures on the other hand show the forces acting upon them by differentiating out tension and
compression vectors into separate components. Most are based upon iterations of regular geometric forms known as
the five Platonic Solids. Complete triangulation and full stability occurs in only three of these, the tetrahedron,
octahedron and icosahedron and these are the best candidates for modeling anatomy. Without triangular bracing, the
cube and the dodecahedron are inherently unstable. All five convex regular polyhedrons demonstrate faces, edges and
angles that are congruent, that is, all faces are equilateral, all angles are the same and all the edges are identical.




Platonic Solids

But as Fuller pointed out, the Babylonians, Egyptians and Greeks modeled their geometry on the mistaken notion that
objects were solid, planes were smooth and bounded by edges, and edges met at a point. Physics discloses no evidence
of a continuum; reality looks and behaves more like a tensegrity– aggregates of non–solid events mediated solely by
tension and compression vectors of force. Further, no two events pass through the same point – rather the tension and
compression vectors twist past each other lending torque or rotation to geometry. Tensegrities always possess
clockwise and counterclockwise rotations of compression and tension that additively cancel each other out to
Guarantee stability.
Tensegrity models of the Platonic Solids can reveal the forces that act on their forms. By studying the geometry of the
body it seems likely that appropriate tensegrity forms can similarly be used to model the forces acting upon it and to
explain systemic function and dysfunction. Of the three regular triangulated polyhedra only the octahedron could be said to possess symmetry in all three axis. A tensegrity version of this called an expanded octahedron is the appropriate model to use where we find these symmetries in the body.
Other classes of tensegrities are chiral, that is they come in left and right–handed versions of what look like skewed or rotated prisms. These seem more appropriate as asymmetrical models of the hands and feet.
In living structure, stability is paired with mobility and objects that are adapted to allow movement possess degrees of
freedom and are not fully triangulated. Degrees of freedom refer to the number of different ways in which a rigid object can move in three dimensions (six). They are: movement up and down (heaving), movement left and right (swaying), movement forward and backward (surging), angling up and down (pitching), turning left and right (yawing) and tilting side to side (rolling). A mechanism or linkage connecting more than one object may have more than the degrees of freedom for a single rigid object. The human arm for example is considered to have seven degrees of freedom, three at the shoulder, one at the elbow and three at the wrist. Controlling degrees of freedom means increasing the stability of an object and in any joint all other unwanted degrees of freedom are constrained by a
combination of bone geometry and connective attachments.
Because tensegrities are never completely rigid, they have varying degrees of freedom whose range of motion is
determined by their triangulation. In this respect they are superficially more similar to plants than to mobile beings.
They can flex and accommodate to vectors of force by slightly altering shape. They bend rather than break. But the
peripheries of the body demonstrate wide ranges of motion that vary in each joint. For tensegrities to emulate anatomy
there must be an increase in ranges of motion without sacrificing stability or degrees of freedom.
In medical terminology, range of motion is the measurement of the distance achievable between the flexed position
and the extended position of a particular joint or muscle group usually measured in degrees. But there’s no talk of
articulation in tensegrity’s definitions. In fact if you look at Fuller and Snelson’s tensegrities, they approximate a
sphere, dome or a mast – there are no joints. The larger they are and the more they weigh, the more load stress is
added to the prestress and the less range of motion they possess. This is key in attempting to find a fit between
anatomy and tensegrity. How does the concept, principle and theory relate to the complex arrangement of irregular
shaped bones, and the fascia, ligaments and tendons that act across articulating joints in our bodies?
One attempt to answer this conundrum, models the actual shape of the bones with their attachments as tensegrities.
There is a direct relationship between an applied load and the morphology of bone. Wolff’s Law of bone transformation says that every change in the function of a bone is followed by certain definite changes in internal architecture and external conformation in accordance with mathematical laws. This means that the external shape of a bone is well adapted to the forces placed upon them. In other words, the geometry of the bone demonstrates that form follows function.
5.) This can be demonstrated using a tensegrity model that diagrams the forces vectors passing through bone. If a bone and it’s attachments (e.g. the femur) can be described as a tensegrity that interacts with another (e.g.the tibia) then any joint can be seen as the interface between two tensegrities. Taken together they form an articulating tensegrity that is greater than the sums of their individual behaviors. Because the components of tensegrities (compression and tension members) can each be thought of as composed of smaller tensegrities, the body is seen as fractal and hierarchical. The body as a whole is always synergistically involved in the actions of the peripheries.
Equally, articulations of successive joints such as fingers, wrist, elbow, shoulder do more than just add up– their effect
is multiplied.
Geometry of the Body
The core of the body, the torso is probably the easiest to model using tensegrity principles. It has bilateral symmetry, oscillates (breathes) and is bounded on all sides by bony structures. Breathing causes the thoracic cage to expand and
contract following the pumping action of the diaphragm.
By abstracting the shape somewhat it is feasible to map the
force vectors of the torso onto an expanded octahedron tensegrity (each of the three axis of the octahedron have been
doubled and separated creating a void within).

Modified X-Octa Tensegrity
This is one of very few tensegrities that exhibit symmetry in three planes and it is well suited to model the torso. This
tensegrity contracts and expands in the same way the torso does and there is a central cavity, as found in the body,
created by the geometry. As two parallel struts are pulled apart (equivalent to e.g. the expansion of the ribs) both other
parallel pairs counter intuitively expand and pull away from each other as well. When a load is imposed, like a weightlifters body at the moment of a lift, the tensegrtity tightens by rotating down and gets smaller. Built from only six struts (suitably modified) they correspond to the boundary planes of the torso– the transverse planes of the clavicle and the pelvis, the coronal planes of the spine and sternum, and the sagittal planes of the ribs on both sides. As well as these bilateral relationships, the compression members also have eight trilateral associations. As in all tensegrities, the torques generated in the triangular relationships all cancel out. There are eight turbining tensioned triangles, four clockwise and four counterclockwise which correspond to eight sections of the torso. Additionally the range of motion and degrees of freedom of the expanded octahedron tensegrity closely matches the torso. The actual geometry (and anatomy) is more complex but the pattern is discernable. If this is a valid comparison, it is worthwhile to examine the musculature to identify helical rotations in these areas and use the behavior of the model to make predictions.
Geometry of the Spine
Years ago I noticed a resemblance between individual thoracic vertebrae and stellated tetrahedrons.

Stellated Tetrahedron Tensegrities
This intrigued me as stacked stellated tetrahedrons can be suspended in a tensile system to form flexible yet stable
tensegrity masts. In the vertebrae the angle between the spinous process and the anterior inferior vertebral body form
two arms of a tetrahedron; the other two arms are the transverse processes. A tensegrity mast, like the spine functions whether vertically or horizontal and can accept loads in any position.

Tensegrity Spine
The spinous process of a superior thoracic vertebra depends below the transverse processes of an inferior vertebra and
may allow for a partial tensegrity suspension. But in the cervical and lumbar vertebrae the geometry is different and harder to envision. The articular facets in the lumbar are angled to support a suspensory load and the nuchal and thoracolumbar fascia may play a part in addition to ligaments and muscles.
More analysis is needed to ascertain what
part tensegral suspension plays in support of the vertebral array. In any case, the intervertebral discs which act as
couplers can also be modeled as tensegrity cushions that can accept and transfer loads.

Tensegrity Disc
The vertebral body is also somewhat compressible much like a stiff spring (and can be modeled by tensgrity prisms).
Tensegrities upon tensegrities inside larger tensegrities… a model complex enough to describe the actual behaviors of
the spine.
Geometry of the Pelvis
As the pelvis also displays bilateral symmetry, another modified expanded octahedron can be added to the torso to
represent the ilia and providing a connection for the femurs.

Tensegrity Torso and Pelvis
The pelvis is a complicated structure and this solution is highly abstract. It is oriented along the familiar 'x, y, and z'
axis' and is schematic of the pelvis which has equivalent orientations (left/right, top/bottom, front/back).
The horizontal struts (x, z) illustrate the dynamic balance of the ilia in relationship to the spine and femurs that are
represented by the vertical (y axis) struts.


Tensegrity Pelvis Balanced and Unbalanced.
Patho-mechanics of the pelvis and lower back are illustrated by shortening or lengthening individual tension members
that are equivalent to hypo- or hyper-tonicity of part of the pelvic musculature. Using this model, it is possible to
distort one or more tensile components (ligaments/muscles) and observe the overall effect on the structure.
Note that a change of length (or tension) in only one tensile component (e.g. the sacroiliac ligament or pelvic floor)
causes distortions to occur throughout the structure in all three axes.
This model illustrates that a change in length of a
tension component is equivalent to an increase or decrease of mobility in that area of the body.
This model also demonstrates gait. As the femur struts (z axis) articulate, simulating walking, the corresponding torque in the struts (x, y axis') demonstrate the rotation in the ilia.
By distorting a single tension element you can then
observe the corresponding distortion in gait.
A more complex look at the geometry strongly suggests that the pelvis is organized as an octet truss. Octet trusses are
omni triangulated space frames composed of octahedrons and tetrahedrons in a close packing array. It is an extremely strong, lightweight structure that distributes forces along the six axes that form the edges of the linked polyhedra. It has been used extensively in truss–supported roofs for very large buildings but the mechanical advantages are independent of scale.
Tensegrity Pelvis Unbalanced
Note that a change of length (or tension) in only one tensile component (e.g. the sacroiliac ligament or pelvic floor)
causes distortions to occur throughout the structure in all three axes. This model illustrates that a change in length of a
tension component is equivalent to an increase or decrease of mobility in that area of the body.
This model also demonstrates gait. As the femur struts (z axis) articulate, simulating walking, the corresponding torque in the struts (x, y axis') demonstrate the rotation in the ilia. By distorting a single tension element you can then observe the corresponding distortion in gait.
A more complex look at the geometry strongly suggests that the pelvis is organized as an octet truss. Octet trusses are
omni-triangulated space frames composed of octahedrons and tetrahedrons in a close packing array. It is an extremely strong, lightweight structure that distributes forces along the six axes that form the edges of the linked polyhedra. It has been used extensively in truss–supported roofs for very large buildings but the mechanical advantages are independent of scale.

Octet Truss
Each Ilium is a tetrahedron hinged at the pubis and the sacrum. The pubis ramus’ and the ischial tuberosity define a triangular plane that is rotated approximately 90 degrees to the plane of the iliac fossa and crest. These planes form a clear tetrahedral relationship. The spacing between the ilia creates an octahedral cavity of which the sacrum forms a face. The remainder of the geometry is filled in with ligaments and muscles of the pelvic floor.

Each Ilium is a tetrahedron hinged at the pubis and the sacrum. The pubis ramus’ and the ischial tuberosity define a
triangular plane that is rotated approximately 90 degrees to the plane of the iliac fossa and crest. These planes form a
clear tetrahedral relationship. The spacing between the ilia creates an octahedral cavity of which the sacrum forms a
face. The remainder of the geometry is filled in with ligaments and muscles of the pelvic floor.

This is exactly the same relationship that two tetrahedron have to an octahedron in an octet truss.
A tensegrity model of this arrangement can demonstrate the linked yet flexible range of movement in the pelvis and
the forces acting through the bones, ligaments and muscles.

Octet Pelvis

Tensegrity Octet Pelvis
It could be said that geometry describes an arrangement in space and tensegrity shows how it is constructed. As befits
their complex character, there is always more than one way to string a tensegrity. In other words this model is an
approximation and a best guess. Other solutions to the observed geometry are possible.
Geometry of a Joint
The attempt to model the range of movement and degrees of freedom of our limbs is the litmus test of the
biotensegrity hypothesis. As noted, the traditional definition of tensegrity does not include joints. Further, the prestress
can be so high that it is difficult to imagine how a tensegrity joint could be fluid. Kenneth Snelson, who is more than a
theoretician, builds tensegrities and understands the problem. He remarked to me that “x with tensegrity it's hard to
manage all the prestressed tension lines in order to control motion dynamically in the way our muscles enable all of
the bodily swings, rotations, pushes, pulls, and their variations.“ But there is a way to proceed. Using a (tetrahedral)
tension sling it is possible to link discrete tensegrity geometries (as discussed) together to form a universal joint. A
tetrahedral ‘saddle joint’ has two degrees of freedom and a wide range of motion in two planes ninety degrees apart.
Tetrahedral Saddle Joint

If one degree of freedom is constrained the resultant hinge begins to move like the knee, except it hyper extends both
posteriorly and anteriorly. Judicious tweaking of geometry brings the model more in line with knee movement. Close
examination of the condyles of the femur and the eminence of the tibia reveals the forces acting upon them and show a
plausible saddle relationship that can be modeled as two tensegrities interdigitating.

Tensegrity Knee Saddle Joint
Tensegrity Knee Construction

Two modified expanded octahedrons rotated 90 degrees to each other axially shows a remarkably close fit to the
geometry of the knee.
In addition the patella is a tetrahedral shaped bone that nests in a gap between the femur and tibia, its position
maintained by another saddle tension sling between the condyles of the femur. For the purposes of this simplified
model the fibula is considered part of the tensegrity of the tibia.
Tensegrity Knee Bent

But how to effect fluid yet controlled movement? Adding a second layer of tension that crosses a joint or joints without being required to carry the entire prestress load, would allow range of movement in an arm or a leg. The prestress of the two tensegrities is not additive and does not cross the joint so it moves freely.
The assumption is that the ligaments and fascia act as deeper layers of tension that carry the prestress and the muscles
stabilize (degrees of freedom) but also are free to operate across the interface (range of motion). Again more research
is needed.
Tensegrity Prisms
A class of chiral (mirror image) tensegrities known as T–prisms illustrates helical forces that act like non–linear
springs. They can be knitted together in contiguous layers to any length and any girth.
Spiral Tensegrity Mast

Tensegrity Foot Construction

Clockwise or counterclockwise, single layer, fourfold T–prisms are appropriate to describe the weight transfer from
the leg to the foot. The talus distributes the loading both posteriorly onto the calcaneus and anteriorly onto the
navicular and other tarsal bones. The geometry of T-prisms is similar : it makes a credible shock absorber and the
helical rotation as it compresses, mimics the pronation of footfall. Stored energy is then released as it expands
providing rebound.
They compress along the vertical axis because their triangulation is hybrid and incomplete, (partly compressive and
partly tensile) but can be strengthened by adding components to add any degree of stiffness.
What Next?
I’ve tried to convey some of the inner workings of tensegrities in this cursory look at applying Biotensegrity to the geometry of anatomy. My observations and ideas are speculative and my models approximate; more needs to be done to fill in the details. As the investigation is just beginning, I am interested in how this will be received over time in the larger medical community. Owing to the power of the idea and thanks to the writings and presentations of Fuller,
Snelson, Ingber, Levin and many others, it appears certain that tensegrity ideas are going to influence the next generation of scientists and artists. My intent is to provide some of the means to further the discussion along productive and scientific lines.
I do not pretend to be doing science; rather I’m laying out the groundwork for future scientific research and investigations. Ultimately if it is a good fit, I would expect to see existing and future healing methodologies incorporating the insights and strengths of tensegrity in their techniques and applications.
New biotensegrity iterations are under way and I invite interested people to contact me with their comments and
suggestions. Studies include explorations into related fields such as prosthetic design, exoskeletons, and robotics. The
advantages of tensegrities are so obvious (strength, resilience, weight) that I expect they will play a key role in future
advances in these and other technologies.
Final note: even as bodies are treated as wholes, so they are embedded in their social and physical matrix and play
their parts in the skein of a larger tensegrity community. But that’s for Carlos Castenada and Stafford Beer to sort
out...
All photos and illustrations copyright T.E. Flemons 2006
1. Salvadori, Mario, 1980, Why Buildings Stand Up, Norton, pp 83–84
2. Wikipedia, http://en.wikipedia.org/wiki/Tensegrity
3. Fuller, R. Buckminster, 1975, Synergetics, Macmillan, pp 372
4. Kenneth Snelson, Interview, http://www.kennethsnelson.net/faqs/faq.htm#1
5. Netter, FH, 1987, Volume 8 Musculoskeletal System, pp 187
Copyright © T.E. Flemons 2007

Orthopedisch chirurg Stephen M. Levin
Potomac Back Center
1577 Spring Hill Road, Suite 203
VIENNA, Virginia 22182
USA
https://www.youtube.com/watch?v=U-47iKNtp88&t=29s
A new model is proposed that accounts for both the statics and the dynamics of the sacrum in vertebrates. The sacrum is viewed as the hub of a tension network. It can act as the support base of the spinal "column" and play an integral role in spinal movement.
Biologic structure must obey all the rules of physics and mechanics. There can be no exceptions. The intricacies of pelvic mechanics should not be a mystery. The laws of physics acting on a body in space are well known and the methode of applying these laws have been standardized.
A common approach in biomechanics is to look at the anatomy and try to decipher the role it plays in body stability and movement. An alternative method might be to envision the requirements necessary to perform a function and then try to understand how this is done by the organism. Often the kinematics (movement without regard to forces) is studied without an understanding of the kinetics (the forces affecting movement). Even less attention is paid to statics (the equilibrium of bodies at rest). Since, first, the body must exist as a structure, stable and fixed in space, it seems logical to try to understand the statics before we act to the dynamica. The sacrum may be the hub of activity and stability, at least in bipeds, and therefore seems a likely subject to investigate. It appears to be the base of the load bearing column, the spine. The load bearing column or wall of a building is the most rigid and rigidly fixed member of that structure. It's base must be on firm footing. The rigidity of structure necessary to bear loads and forces is the antithesis of flexibility needed for movement. What are the forces that stabilize the sacrum and how can the rigidly stable sacrum then move without the body structure collapsing?
A standard engineering tool for determining forces acting on a body stable in space is to construct a free body diagram. This disembodied structure diagrammed to show the forces acting upon it. Known forces acting on the body are diagrammed as vectors of force and the counter balancing forces that keep the body fixed in space can then be calculated. In a Cartesian coordinate system a free body can rotate around three axes (x,y,z) and translate in three planes (xy,xz,yz).
White end Panjabi, use this concept when describing spinal mechanics and it is now widely used in the biomechanics literature for describing movement and forces in the musculoskeletal system. Convention labels these movement possibilities six degrees of freedom. However, in biomechanics it seems more logical to describe twelve degrees of freedom(, six positive and six negative. A body can be described as rotating positively or negatively around an axis or translating in a plane positively (clockwise) or negatively (counterclockwise).


Figure 1: The right-handed Cartesian orthogonal coordinate system. The point of intersection of the three axes here the sacrum), is called the origin The positive and negative translations and rotations are defined by convention .
Usually the interactive forces within the parent structure are ignored, for simplicity, so that only the forces of gravity and external applied forces are considered. This works out well in buildings and similar structures as it is usually clear as to what are the interactive forces and they can be readily calculated. In biologic structures the problem is more confusing as the members of the whole organism are highly interactive.
The force generated by the biceps muscle is then readily calculated. But the biceps is a two joint muscle and as it contracts it creates a moment around the gleno-humeral joint that is not part of the free body diagram. The gleno-humeral joint would have to be stabilized to keep the elbow from flying off in space. The triceps muscle would contract to do this (out of the diagram) but this would then put an extensor force on the elbow (back to the diagram). This would have to be counterbalanced by the biceps in a feedback loop, throwing off all previous calculations. It would do no good to include the gleno-humeral joint in the original free body diagram as the forces on the scapulo-thoracic joint would have to be reckoned with and so on.
As a more fundamental problem we should consider how can be stabilize a free body in space? Since there are twelve degrees of freedom (six positive and six negative) logically twelve restraints are necessary. Fuller shows that a bicycle wheel needs a minimum of twelve spokes to stabilize its hub (a fact well know to bicycle repair persons) and proves that twelve restrains are necessary to fix a point in space Like a tent secured by its guy ropes, no additional tethers are necessary no matter that way the wind blows. Once rigidly fixed in space external forces may change the magnitude but not the direction of the vectors.
What are the forces necessary to stabilize the sacrum? A sacrum has mass and, like an airplane on the deck of an aircraft carrier, has to be tethered to keep it in place.
The sacrum, tethered in three-dimensional space, can be rigidly restrained by twelve tension vectors. It would be suspended in the myofascial soft tissue network, like the hub of a wire bicycle wheel suspended by the spokes. Like the wire wheel, many additional "spokes" or tension elements can provide a fail-safe mechanism but confuse the picture a bit. Grant and Kapandji diagram the ligaments of the pelvis showing counterbalancing tension forces consistent with this concept. The ligaments and myofascial components that attach to the pelvis must act as tension tethers, fixing the sacrum in its position in the body. Additional constraints such as those discussed by Vleeming exist but may be species specific and not a structural requirement. A wire wheel modeled sacrum is omnidirectional and functions equally well when the load is applied from any direction. It depends on the intrinsic tension of the ligaments and muscles and not on gravity as a stabilizing force, in contrast to "keystone" and similar models. Since it does not depend on gravity to hold it in place the sacrum functions equally well right side up, upside down or sideways. A tension fixed sacrum functions on land, in the air, at sea or in a gravity free environment, space. It would work as the model for bipedal and quadrupedal stability and motion and therefore, becomes the most widely adaptable of proposed models.
Like the hub of a wire wheel suspended by its spokes, there has to be a dynamic balance of the tension structures as part of a system. A load on the wheel hub does not change the relative position of the hub within the rim. If the tension of the spokes remains constant the hub moves not at all. Assuming a minimum of twelve properly vectored constraints, the hub is rigidly fixed.
To move the hub the opposing positive-negative spokes would have to be Iengthened shortened or removed to allow the hub to move back and forth like a diaphragm.
Ligaments of the body have very high tensile strength and could not distort much. The sacrum, as a hub, would move in harmony with the other bones of the pelvis, moving in and out like a diaphragm or rotating in a fixed relationship to the other bones . It is controlled by antagonistic muscles and by the tensile ligaments. For the most part, the ligaments have been ignored as prime movers in the body. Dorman has proposed a clockwork mechanism in which the ligaments play a dynamic role in the walking cycle with particular attention to the ligaments role in pelvic mechanics. Stored energies in the ligaments are the torsion bars of the pelvis.
The mechanism of a double tie bar hooked in series and the dynamic interaction of ligaments is apparent in a "Jacob's ladder", an ancient toy.

Jacobs ladder
Jacob's ladder. A crossed tie bar toy that demonstrates knee cruciate ligament action and seri al interactions of a chain of tie bars.
Flexing one rigid block creates a kinetic chain that sends all the blocks in a controlled tumble, precisely organized by the controlling tension elements. These tension elements do not shorten or lengthen but, nevertheless, force the rigid blocks to move. If the end blocks are held so that tension is created through the system the tumbling effect can move top to bottom, bottom to top, horizontally or at any angle.
In the spine this type of movement has been described as coupled movement. Friette describes this movement in detail. However, the mechanical explanation for this movement pattern in the spine has been missing. If a double tie bar hinge exists in the spine, as it does in the knee, this coupling can be readily explained. The cruciale ligament arrangement is very apparent in the microscopic and macroscopic organization of the annulus of the disk. it is also seen in the three layers of transverso-spinales muscles and the costo-transverse ligaments and the lumbar fascia.
In this Jacob's Ladder model of the spine rotating the head or sacrum around the x,y or z axis would create obligatory movements of the entire spine in a very controlled pattern. The only actively contracting muscles (that could be seen by EMC; studies) would be those needed to rotate the head or tail. The intrinsic tone of the ligaments and muscles of the discs and vertebrae controle the rest of the spine's movement.
When walking the head tends to stay level and directed forward. It is the sacrum, wound by the counter rotating ilia, which moves the spine. The vertical lift when walking imparts potential energy stored in the ligaments of the twisting ilia that then becomes the kinetic energy that powers the sacrum. As pointed out by Grecovetsky and Dorman the limbs are propelled out from the central core like the arms of a vertical pendulum or a tetherball being unwound and rewound around its pole. It is the tension in the ligaments and muscles, preset like the spokes of a bicycle wheel, that control both the stability and the movement pattern of the "spinal engine" described by Grecovetsky.
Wire wheel-like structures have been termed "tensegrity"˚ (for tension integrity) by Buckminster Fuller. This is a class of constructs where the compression elements, the rim and the hub, are separated from each other and transmit the forces between them through these tension elements. According to Fuller the compressional "islands" are interpositioned in structural stability only by the tensional spokes. "Tension is primary and comprehensive and compression is secondary and local". The tensegrity icosahedron is used by Wang and Imber as the model for cell structure .
Levin proposes that the tension icosahedron is the primordial biomechanical structure. A hierarchical system of tension icosahedrons is used by Levin to model both the statics and dynamics of the body efficiently, with least energy costs. The wire wheel pelvis and the Jacob's ladder spine are tensegrity structures. Tension elements coming from the icosahedron's twelve vertices would rigidly tether a central hub . The bones would be compression islands fixed in a tension network. Using this model the sacrum is fixed in three-dimensional space because it is part of an integrated tensegrity structural system. Although its relationships between it and other bones remain fixed it also moves. It may control the movement of the other bones in movement patterns such as walking, just as the front wheel of a bicycle affects the rear wheel. It may be the central force in these movements, the Chi in the ancient Chinese concept.
CONCLUSION
A model for sacral mechanics is proposed that is consistent with mechanical laws and observed anatomical function. This model performs equally well in describing the statics and dynamics of the sacrum. It provides for stability of the sacrum when it is loaded from any direction and can be utilized during bipedal or quadrupedal standing and walking or even standing on ones' head. It is a low energy requiring system and therefore à fortiori favored by nature. This sacral model is consistent with an integrated systems model of biomechanics previously proposed.